Question

A uniformly charged conducting sphere of 0.10 m diameter has a surface charge density of 150 µC/m2. This sphere is sitting at the center of a box that is cubic with sides of 0.30 m’s.

(a)What is the electric flux through one of the sides of the containing box? (assuming the box has no net charge)

Answer 1

8.85 x 10⁴ Nm²/C

Step-by-step explanation:

d = diameter of the conducting sphere = 0.10 m

r = radius of the conducting sphere = (0.5) d = (0.5) (0.10) = 0.05 m

Area of the sphere is given as

A = 4πr²

A = 4 (3.14) (0.05)²

A = 0.0314 m²

σ = Surface charge density = 150 x 10⁻⁶ C/m²

Q = total charge enclosed

Total charge enclosed is given as

Q = σA

Q = (150 x 10⁻⁶) (0.0314)

Q = 4.7 x 10⁻⁶ C

Electric flux through one of the side is given as

`\phi = (Q)/(6\epsilon _(o))`

`\phi = (4.7* 10^(-6))/(6(8.85* 10^(-12)))`

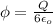
`\phi` = 8.85 x 10⁴ Nm²/C