Question

Initially, there were only 86 weeds in the garden. The weeds grew at a rate of 29% each week. The following function represents the weekly weed growth: f(x) = 86(1.29). Rewrite the function to show how quickly the weeds grow each day.

A.f(x) = 86(1.04)*; grows approximately at a rate of 0.4% daily

B.f(x) = 86(1.04)7%, grows approximately at a rate of 4% daily

C.f(x) = 86(1.29)7%; grows approximately at a rate of 20% daily

D.f(x) = 86(1.297); grows approximately at a rate of 2% daily​

Answer 1

not sorry, but guy above is w.r.o.n.g

0.4 ain't right

yw for saving you an attempt

Answer 2

Option A.
`f(x)=86[1.04]^(x)` ; grows approximately at a rate of 0.4% daily

Explanation:

we have

`f(x)=86(1.29)^(x)`

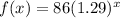
where

f(x) the number of weeds in the garden

x ----> the number of weeks

Calculate how quickly the weeds grow each day

Remember that a week is equal to seven days

so

`f(x)=86(1.29)^{(x)/(7)}`

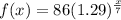
Using the law of exponents

b^(x/a) = b^(x*(1/a)) = (b^(1/a))^x

so

`f(x)=86[(1.29)^{(1)/(7)}]^(x)`

`f(x)=86[1.04]^(x)`

therefore

The rate is approximately

1.04=1+r

r=1.04-1=0.04=4% daily