Answer:
The graph of g(x) is equal to the graph of f(x) shifted 3 units to the right and 4 units above.
Explanation:
we know that
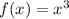 ----> the turning point is the point (0,0)
----> the turning point is the point (0,0)
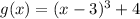 ----> the turning point is the point (3,4)
----> the turning point is the point (3,4)
The rule of the translation of f(x) to g(x) is equal to
(x,y) ------> (x+3,y+4)
That means-----> The translation is 3 units at right and 4 units up
therefore
The graph of g(x) is equal to the graph of f(x) shifted 3 units to the right and 4 units above.