It's not true for any
 , but it is for
, but it is for
 .
.
Start with
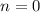 (which is even). Then
(which is even). Then
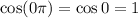
The cosine function is
![2\pi[tex]-periodic, meaning that for any [tex]x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x35x6gf5u87cyhct1kkwsx0c2e17dd4wox.png) we have
we have
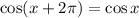
Now,
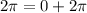 , so
, so
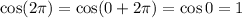
This is the basis for an argument via induction to show that
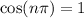 whenever
whenever
 is even. Also, when
is even. Also, when
 is even we have
is even we have
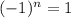 .
.
In a similar way, starting with the fact that
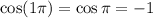
and that
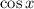 is periodic, we have
is periodic, we have
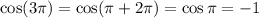
and so for odd
 we have
we have
 .
.