Question

A simple random sample of 60 is drawn from a normally distributed population, and the mean is found to be 28, with a standard deviation of 5. Which of the following values is within the 95% confidence interval (z-score = 1.96) for the population mean? Remember, the margin of error, ME, can be determined using the formula ME=z*s/square root n. The value of 26, because it’s not greater than 26.7 and less than 29.3. The value of 27, because it’s greater than 26.7 and less than 29.3. The value of 32, because it’s greater than 23 and less than 33. The value of 34, because it’s not greater than 23 and less than 33.

Answer 1

B.The value of 27, because it’s greater than 26.7 and less than 29.3.Explanation:

Answer 2

The value of 27, because it’s greater than 26.7 and less than 29.3.

Explanation:

You should find the confidence Interval at 95%

The formula to apply is;

C.I= x±z*δ/√n

where C.I is the confidence interval, x is the mean of the sample, z is the z* value from the standard normal distribution for 95% confidence interval, δ is the standard deviation and n is the sample size

Substitute values in the formula

`z*=1.96\\\\`

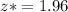
Find δ/√n

`=(5)/(√(60) ) =0.64549722436\\\\\\`

Calculate z*δ/√n

`=1.96*0.64549722436=1.2652\\\\\\`

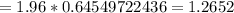
C.I= 28±1.2652

Upper limit is = 28+1.2652=29.2625

Lower limit is =28-1.2652=26.7348

Solution

The value 27 is within 95% confidence interval because it is greater than 26.7 and less than 29.3