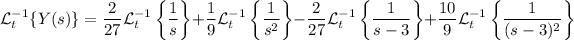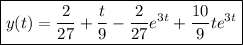Question

Por favor ayuda con estw problema de la transformada de ls derivada

Y''-6y+9y=t y(0)=0 y' (0)=1

Answer 1

Parece que refieres a la transformada de Laplace. Aplica la transformada a los lados ambos de la ecuación diferencial:

`\mathcal L_s\{y''(t)-6y'(t)+9y(t)\}=\mathcal L_s\{t\}`

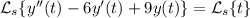
Denota por
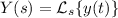`Y(s)=\mathcal L_s\{y(t)\}` la transformada de
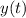`y(t)`. En el lado izquierdo obtenemos

`\mathcal L_s\{y''(t)-6y'(t)+9y(t)\}=\mathcal L_s\{y''(t)\}-6\mathcal L_s\{y'(t)+9\mathcal L_s\{y(t)\}`

`\mathcal L_s\{y''(t)-6y'(t)+9y(t)\}=(s^2Y(s)-sy(0)-y'(0))-6(sY(s)-y(0))+9Y(s)`

`\mathcal L_s\{y''(t)-6y'(t)+9y(t)\}=(s^2-6s+9)Y(s)-1`

`\mathcal L_s\{y''(t)-6y'(t)+9y(t)\}=(s-3)^2Y(s)-1`

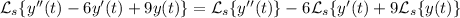
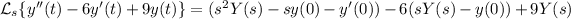
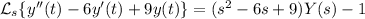
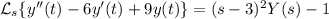
y a la derecha,

`\mathcal L_s\{t\}=\frac1{s^2}`

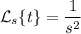
Ahora resuelve para
`Y(s)`:

`(s-3)^2Y(s)-1=\frac1{s^2}`

`(s-3)^2Y(s)=1+\frac1{s^2}`

`Y(s)=(s^2+1)/(s^2(s-3)^2)`

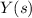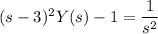
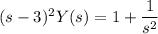
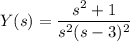
Expande la fracción por la derecha en fracciones parciales; busque
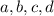`a,b,c,d` tal que

`(s^2+1)/(s^2(s-3)^2)=\frac as+\frac b{s^2}+\frac c{s-3}+\frac d{(s-3)^2}`

`s^2+1=as(s-3)^2+b(s-3)^2+cs^2(s-3)+ds^2`

`s^2+1=(a+c)s^3+(-6a+b-3c+d)s^2+(9a-6b)s+9b`

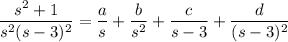
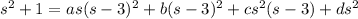
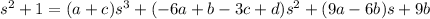
Emparejando los términos con igual grado da el sistema con soluciones

`\begin{cases}a+c=0\\-6a+b-3c+d=1\\9a-6b=0\\9b=1\end{cases}\implies a=\frac2{27},b=\frac19,c=-\frac2{27},d=\frac{10}9`

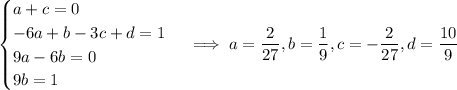
Pues

`Y(s)=\frac2{27}\frac1s+\frac19\frac1{s^2}-\frac2{27}\frac1{s-3}+\frac{10}9\frac1{(s-3)^2}`

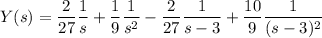
y tomar la transformada inversa es trivial. Obtenemos

`\mathcal L^(-1)_t\{Y(s)\}=\frac2{27}\mathcal L^(-1)_t\left\{\frac1s\right\}+\frac19\mathcal L^(-1)_t\left\{\frac1{s^2}\right\}-\frac2{27}\mathcal L^(-1)_t\left\{\frac1{s-3}\right\}+\frac{10}9\mathcal L^(-1)_t\left\{\frac1{(s-3)^2}\right\}`

`\boxed{y(t)=\frac2{27}+\frac t9-\frac2{27}e^(3t)+\frac{10}9te^(3t)}`