Question

Island A is 230 miles from island B. A ship captain travels 260 miles from island A and then finds that he is off course and 200 miles from island B. What bearing should he turn to, so he is heading straight towards island B?

A. 121.73
B. 152.5
C. 31.73
D. 50.45

Answer 1

A.) 121.73

Explanation:

I got it correct on founders edtell

Answer 2

Option A) 121.73

Explanation:

The given scenario can be represented by a Triangle ABC attached in the image below.

We have 3 sides of the triangle ABC, using the measure of these sides we can find the angle opposite to side c which will help us in finding the measure of bearing.

Law of cosine relates the 3 sides of the triangle and angle opposite to one side by following equation:

`c^(2)=a^(2)+b^(2)-2abcos(C)`

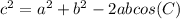
Using the values of a,b, and c we get:

`230^(2)=200^(2)+260^(2)-2(200)(260)cos(C)\\\\2(200)(260)cos(C)=200^(2)+260^(2)-230^(2)\\\\ cos(C)=(200^(2)+260^(2)-230^(2))/(2(200)(260))\\\\ cos(C)=(547)/(1040)\\\\ C=cos^(-1)((547)/(1040))\\\\ C=58.267`

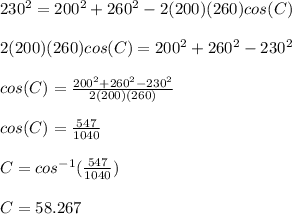
Thus, the measure of angle C comes out to be 58.267 degrees. The angle with which the boat will have to turn will be:

180 - 58.267 = 121.733 degrees.

Therefore, option A is the correct answer