Question

Which of the following options is a polynomial with a root 2i and exactly 2
real roots?

Answer 1

B.
`f(x)=x^4-x^3+2x^2-4x-8`

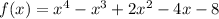
Explanation:

If
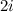`2i` is a root of f(x), then the complex conjugate
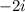`-2i` is also a solution. If f(x) should have exactly 2 real roots, then by the Fundamental Theorem of Algebra, the minimum degree of f(x) is 4.

Hence the first and last options are eliminated.

By the Remainder Theorem,
`f(2i)=0`.

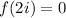Let us check for options B and C.

For option B.

`f(x)=x^4-x^3+2x^2-4x-8`

`\implies f(2i)=(2i)^4-(2i)^3+2(2i)^2-4(2i)-8`

`\implies f(2i)=16i^4-8i^3+8i^2-8i-8`

`\implies f(2i)=16+8i-8-8i-8=0`

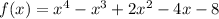
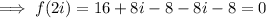
For option C

`f(x)=x^4-x^3-6x^2+4x+8`

`\implies f(2i)=(2i)^4-(2i)^3-6(2i)^2+4(2i)+8`

`\implies f(2i)=16i^4-8i^3-24i^2+8i+8`

`\implies f(2i)=-16+8i+24+8i+8\\e0`

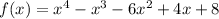
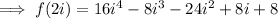
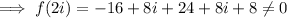
Therefore the correct choice is B.