Answer:
D. 5.7
Explanation:
We have been given that in △ABC,c=12, m∠B=27°, and a=9. We are asked to find the value of b.
We will use law of cosines to solve for b.

Upon substituting our given values in law of cosines, we will get:
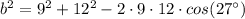
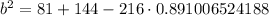
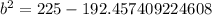
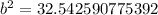
Now, we will take square root of both sides of our equation.
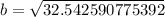
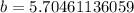
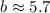
Therefore, the value of b is 5.7 and option D is the correct choice.