Question

Circle A has been dissected into 16 congruent sectors. The base of one sector is 1.95 units, and its height is 4.9 units. What is the approximate area of circle A?

circle A is dissected into 16 congruent sectors, one sector is highlighted
27.52 units2
48.92 units2
75.39 units2
76.44 units2

Answer 1

D.76.44 square units

Explanation:

We are given that

Base of one sector=b=1.95 units

Height of sector=h=4.9 units

Total number of sectors=16

Area of one sector is equal to area of triangle (approximately)

Area of sector=
`(1)/(2)bh`

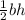
Using the formula

Area of one sector=
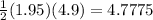`(1)/(2)(1.95)(4.9)=4.7775` square units

Area of circle A=
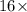`16*`area of sector

Area of circle A=
`16* 4.7775=76.44` square units

Hence,option D is true.

Answer 2

`A=76.44\ units^(2)`

Explanation:

To find the approximate area of the circle, calculate the area of one sector and then multiply by 16

Remember that

The area of a triangle (one sector) is equal to

`A=(1)/(2)(b)(h)`

therefore

The approximate area of the circle is equal to

`A=(16)(1)/(2)(1.95)(4.9)`

`A=76.44\ units^(2)`