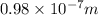Answer:
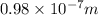
Explanation:
For calculating wavelength, when the electron will jump from n=4 to n= 1
Using Rydberg's Equation: for hydrogen atom
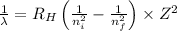
Where,
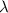 = Wavelength of radiation = ?
= Wavelength of radiation = ?
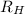 = Rydberg's Constant =
= Rydberg's Constant =
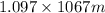
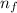 = Higher energy level = 4
= Higher energy level = 4
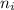 = Lower energy level = 1
= Lower energy level = 1
Z= atomic number = 1 (for hydrogen)
Putting the values, in above equation, we get
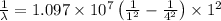
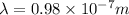
Thus the wavelength of the photon emitted will be