Question

Vector u has a magnitude of 5 units and a direction angle of 30°. Vector v has a magnitude of 7 units and a direction angle of 120°. What is the direction angle of their vector sum?

Answer 1

Nearly 84°

Explanation:

In the attached diagram

• vector AB is vector u with magnitude 5 units
• vector AC is vector v with magnitude 7 units
• angle FAB = 30°
• angle FAC = 120°

So, angle BAC = 120° - 30° = 90°

A parallelogram ABCD is a rectangle, its diagonal vector AD is the sum of vectors AB and AC.

Consider right triangle ABD. In this triangle

`\tan \angle BAD=(BD)/(AB)=(AC)/(AB)=(7)/(5)\\ \\\angle BAD\approx 54^(\circ)`

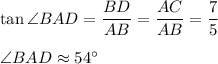
So, the sum vector AD has direction 30° + 54° = 84°