Answer:
The correct option is C) 6√2.
Explanation:
Consider the provided triangle.
The provided triangle is a right angle triangle, in which two angles are 45° and one is 90°.
As both angles are equal there opposite side must be equal.
Thus, the leg of another side must be 6.
Now find the hypotenuse by using Pythagorean theorem:

Substitute a = 6 and b = 6 in
 .
.
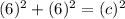
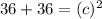
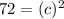
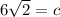
Hence, the length of the hypotenuse in the right triangle is 6√2.
Therefore, the correct option is C) 6√2.