Answer:
D. (x, y, z) = (1, 1, 2). That is:
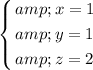 .
.
Explanation:
Step One: Make sure that the first coefficient of the first row is 1. In this case, the coefficient of
 in the first row is already 1.
in the first row is already 1.
Step Two: Using row 1, eliminate the first unknown of row 1
 in the rest of the rows. For example, to eliminate
in the rest of the rows. For example, to eliminate
 from row 2, multiply row 1 by the opposite of the coefficient of
from row 2, multiply row 1 by the opposite of the coefficient of
 in row 2 and add that multiple to row 2. The coefficient of
in row 2 and add that multiple to row 2. The coefficient of
 in row 2 is
in row 2 is
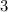 . Thus, multiply row 1 by
. Thus, multiply row 1 by
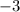 to get its multiple:
to get its multiple:
 .
.
Add this multiple to row 2 to eliminate
 in that row:
in that row:
![\begin{array}{lrrrcr}&-3x &-3y&+3z& =&0 \\ + & 3x& -y& +z& =& 4\\\cline{1-6}\\[-1.0em]\implies&&-4y &+ 4z&=&4\end{array}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2k5pgh7ktysuq3ehznwpv1k98t4epdg9dz.png) .
.
Similarly, for the third row, multiply row 1 by
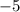 to get:
to get:
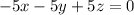 .
.
Do not replace the initial row 1 with this multiple.
Add that multiple to row 3 to get:
![\begin{array}{lrrrcr}&-5x &-5y&+5z& =&0 \\ + & 5x& & +z& =& 7\\\cline{1-6}\\[-1.0em]\implies&&-5y &+6z&=&7\end{array}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kdhzt66iq172xd9t7kx9s6lbnwqtm72pjg.png) .
.
After applying step one and two to all three rows, the system now resembles the following:
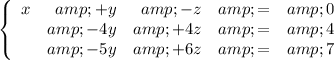 .
.
Ignore the first row and apply step one and two to the second and third row of this new system.
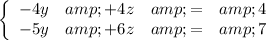 .
.
Step One: Make sure that the first coefficient of the first row is 1.
Multiply the first row by the opposite reciprocal of its first coefficient.
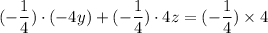 .
.
Row 1 is now
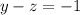 .
.
Step Two: Using row 1, eliminate the first unknown of row 1
 in the rest of the rows.
in the rest of the rows.
The coefficient of
 in row 2 is currently
in row 2 is currently
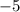 . Multiply row 1 by
. Multiply row 1 by
 to get:
to get:
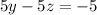 .
.
Do not replace the initial row 1 with this multiple.
Add this multiple to row 2:
![\begin{array}{lrrcr}&-5y&+6z& =&7 \\ + & 5y& -5z& =& -5\\\cline{1-5}\\[-1.0em]\implies&&z &= &2\end{array}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hnu1fbnurp1zbpejk62b0rify0vxjfvcw2.png) .
.
The system is now:
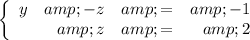 .
.
Include the row that was previously ignored:
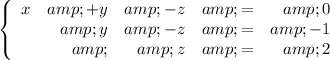 .
.
This system is now in a staircase form called Row-Echelon Form. The length of the rows decreases from the top to the bottom. The first coefficient in each row is all
 . Find the value of each unknown by solving the row on the bottom and substituting back into previous rows.
. Find the value of each unknown by solving the row on the bottom and substituting back into previous rows.
From the third row:
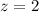 .
.
Substitute back into row 2:
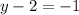 .
.
 .
.
Substitute
 and
and
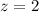 to row 1:
to row 1:
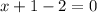 .
.
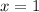 .
.
In other words,
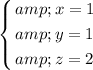 .
.