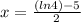Question

Solve: e^2x + 5 = 4
help pls

Answer 1

Answer is C on edge

Explanation:

x= (ln 4)- 5/2

Answer 2

The solution of the equation is
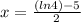`x=((ln4)-5)/(2)` ⇒ 3rd answer

Explanation:

* Lets explain how to solve this problem

- The function f(x) = e^x is called the (natural) exponential function

- The natural logarithm (㏑), or logarithm to base e, is the inverse

function to the natural exponential function

∵
`e^(2x+5)=4` is an exponential function

∴ We can solve it by using the inverse of e (㏑)

- Remember:

#
`ln(e)=1`

#
`ln(e^(m))=m(ln(e))=m`

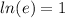
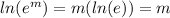
- Insert ln in both sides

∴
`ln(e^(2x+5))=ln(4)`

∵
`ln(e^(2x+5))=(2x+5)ln(e)=2x+5`

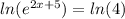
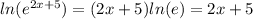
∴ 2x + 5 = ㏑(4)

- Subtract 5 from both sides

∴ 2x = ㏑(4) - 5

- Divide both sides by 2 to find x

∴
`x=(ln(4)-5)/(2)`

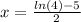
* The solution of the equation is
`x=((ln4)-5)/(2)`