Answer:
There is a 41.67% probability that exactly 4 boys are picked in this team of 5.
Explanation:
The order is not important, so we use the combinations formula.
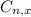 is the number of different combinatios of x objects from a set of n elements, given by the following formula.
is the number of different combinatios of x objects from a set of n elements, given by the following formula.
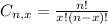
Number of desired outcomes.
Four boys and one girl: So

Number of total outcomes:
Combination of five from a set of 10.
So
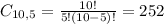
What is the probability that exactly 4 boys are picked in this team of 5?
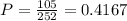
There is a 41.67% probability that exactly 4 boys are picked in this team of 5.