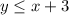Answer:
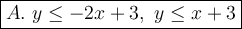
Explanation:
<, > - dotted line
≤, ≥ - solid line
<, ≤ - shaded region below the line
>, ≥ - shaded region above the line
=============================================
The slope-intercept form of an equation of a line:

m - slope
b - y-intercept → (0, b)
The formula of a slope:
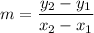
From the graph we have the points:
(0, 3) - y-intercept → b = 3 (for both lines)
f(x)
(0, 3), (1, 1)
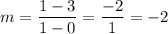
Substitute:
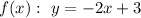
The shaded region is below the solid line. Therefore:
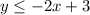
g(x):
(0, 3), (2, 5)

Substitute:
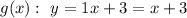
The shaded region is below the solid line. Therefore: