Question

An Earth satellite moves in a circular orbit 561 km above Earth's surface with a period of 95.68 min. What are (a) the speed and (b) the magnitude of the centripetal acceleration of the satellite?

Answer 1

Step-by-step explanation:

It is given that,

Radius of earth, r = 6371 km

An earth satellite moves in a circular orbit above the Earth's surface, d = 561 km

So, radius of satellite, R = 6371 km + 561 km = 6932 × 10³ m

Time taken, t = 95.68 min = 5740.8 sec

(a) Speed of the satellite is given by :

`v=(d)/(t)`

d = distance covered

For circular path, d = 2πR

`v=(2\pi * 6932* 10^3\ m)/(5740.8\ sec)`

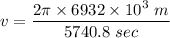
v = 7586.92 m/s

(b) Centripetal acceleration is given by :

`a=(v^2)/(R)`

`a=((7586.92\ m/s)^2)/(6932* 10^3\ m)`

`a=8.3\ m/s^2`

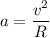
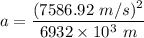
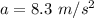
Hence, this is the required solution.