Question

Which inequality matches the graph?


`- 2x + 3y > 7`

`2x - 3y < 7`

`- 3x + 2y \geqslant 7`

`3x - 2y \leqslant 7`
​

Answer 1

`\large\boxed{-3x+2y\geq7}`

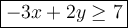
Explanation:

<, > - dotted line

≤, ≥ - solid line

<, ≤ - shaded region below the line

>, ≥ - shaded region above the line

====================================

We have solid line (≤, ≥).

Shaded region is above the line (>, ≥)

Therefore, the inequality sign must be: ≥

Finally, your answer is -3x + 2y ≥ 7.

Check the equation of a line.

The point-slope form of an equation of a line:

`y-y_1=m(x-x_1)`

`m=(y_2-y_1)/(x_2-x_1)`

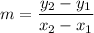
From the graph we ahve the points (3, 8) and (1, 5) - look at the picture.

Substitute:

`m=(5-8)/(1-3)=(-3)/(-2)=(3)/(2)`

`y-8=(3)/(2)(x-3)`

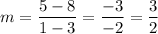
Convert to the standard form
`Ax+By=C`:

`y-8=(3)/(2)(x-3)` multiply both sides by 2

`2y-16=3(x-3)` use the distributive property

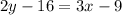`2y-16=3x-9` subtract 3x from both sides

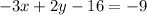`-3x+2y-16=-9` add 16 to both sides

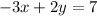`-3x+2y=7` CORRECT :)