Question

Huck and Jim are waiting for a raft. The number of rafts floating by over intervals of time is a Poisson process with a rate of λ = 0.4 rafts per day. They agree in advance to let the first raft go and take the second one that comes along. What is the probability that they will have to wait more than a week? Hint: If they have to wait more than a week, what does that say about the number of rafts in a period of 7 days?

Answer 1

Answer: 0.0081

Explanation:

Let X be the number of rafts.

Given : The mean number of rafts floating :
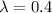`\lambda=0.4` rafts per day .

Then , for 7 days the number of rafts =
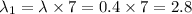`\lambda_1=\lambda* 7=0.4*7=2.8` rafts per day .

The formula to calculate the Poisson distribution is given by :_

`P(X=x)=(e^(-\lambda_1)\lambda_1^x)/(x!)`

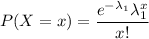
Now, the probability that they will have to wait more than a week is given by :-

`P(X>7)=1-P(X\leq7)\\\\=1-(P(0)+P(1)+P(2)+P(3)+P(4)+P(5)+P(5)+P(6)+P(7))\\\\=1-((e^(-2.8)2.8^(0))/(0!)+(e^(-2.8)2.8^(1))/(1!)+(e^(-2.8)2.8^(2))/(2!)+(e^(-2.8)2.8^(3))/(3!)+(e^(-2.8)2.8^(4))/(4!)+(e^(-2.8)2.8^(5))/(5!)+(e^(-2.8)2.8^(6))/(6!)+(e^(-2.8)2.8^(7))/(7!))\\\\=1-0.991869258012=0.008130741988\approx0.0081`

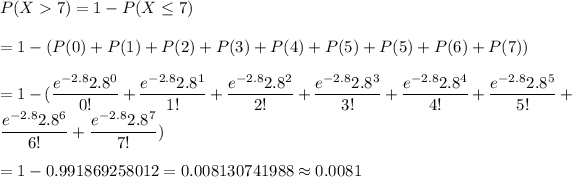
Hence, the required probability : 0.0081