Answer: 0.1841
Explanation:
Given: Mean :
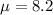
Standard deviation :
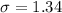
The formula to calculate z-score is given by :_

For x= 9, we have

For x= 10, we have
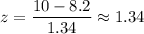
The P-value =
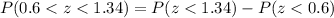
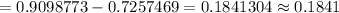
Hence, the probability that at your next exam, you will have a stress level between 9 and 10 = 0.1841