Question

What is the freezing point of water made by dissolving 22.78 g of ethylene glycol (CH2(OH)CH2(OH)) in 87.95 g of water? The freezing-point depression constant of water is 1.86 oC/m.

Answer 1

Step-by-step explanation:

When a non-volatile solute is added in a solvent then decrease in its freezing point is known as freezing point depression.

Mathematically,
`\Delta T = K_(f)m`

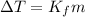
where
`\Delta T` = change in freezing point

`K_(f)` = freezing point depression constant
`\text({in ^(o)C/mol/kg})`

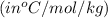
m = molality

First, calculate the number of moles as follows.

No. of moles =
`\frac{\text{mass of solute}}{\text{molar mass of solute}}`

=
`(22.78g)/(62.07 g/mol)`

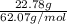
= 0.367 mol

Now, it is given that mass of solvent is 87.95 g. As there are 1000 grams in 1 kg.

So,
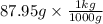`87.95g * (1 kg)/(1000 g)` = 0.08795 kg

Hence, molality of the given solution is as follows.

Molality =
`\frac{\text{no. of moles}}{\text{mass in kg}}`

=
`(0.367 mol)/(0.08795)`

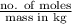
= 4.172 mol/kg

Therefore, depression in freezing point will be as follows.

`\Delta T = K_(f)m`

`T_(solvent) - T_(mixture)` =
`K_(f)m`

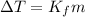
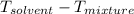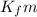
Since, freezing point of pure water is
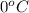`0^(o)C`. Now, putting the given values as follows.

`0^(o)C - T_(mixture)` =
`1.86^(o)C/m * 4.172mol/kg`

=
`-7.759 ^(o)C`

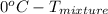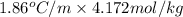
Thus, we can conclude that the freezing point of water in the given mixture is
`-7.759 ^(o)C`.