Question

Suppose the cells of a tumor are idealized as spheres each with a radius of 5 mum ​(micrometers). The number of cells has a doubling time of 35 days. Approximately how long will it take a single cell to grow into a​ multi-celled spherical tumor with a volume of 0.2 cmcubed ​(1 cmequals​10,000 mu​m)

Answer 1

1044.3 days

Step-by-step explanation:

Given,

Radius of sphere shaped cells of tumor
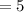`= 5` micrometer

`1` centimeter
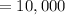`= 10,000` micrometers

Thus, radius of sphere in centimeters

`= (5)/(10,000) \\`

Volume of a sphere

`= (4)/(3) \pi r^(3)`

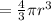
Volume of one cell of tumor

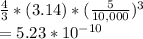`(4)/(3) *(3.14)*((5)/(10,000))^(3)\\= {5.23 * 10^(-10)` centimeter cube

As we know ,

`N(t) = N(0) e^(-kt)\\\\k = (ln2)/(35)\\ k = 0.0198 day^(-1)\\`

Substituting all the given values in above equation, we get -

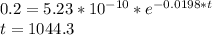`0.2 = 5.23 * 10^(-10) * e^(-0.0198*t)\\t = 1044.3` days