Answer:
Multiply the second equation by -2 to get
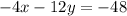
Explanation:
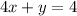
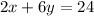
To eliminate one variable the coefficient of a variable should be same with opposite sign.
LEts check with each option
Multiply the first equation by -4 to get
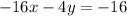
the coefficient of x or y are not same when we compare with second equation
Multiply the second equation by -4 to get

the coefficient of x or y are not same when we compare with first equation
Multiply the first equation by -2 to get

the coefficient of x or y are not same when we compare with second equation
Multiply the second equation by -2 to get
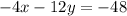
The coefficient of x terms are same with different sign when compare with first equation
So when we add first and second equation , the x will get eliminated.