Question

In the Midpoint Rule for triple integrals we use a triple Riemann sum to approximate a triple integral over a box B, where f(x, y, z) is evaluated at the center (xi, yj, zk) of the box Bijk. Use the Midpoint Rule to estimate the value of the integral. Divide B into eight sub-boxes of equal size. (Round your answer to three decimal places.)triple integrals of cos(xyz) dV,where B = 0 ≤ x ≤ 2, 0 ≤ y ≤ 2, 0 ≤ z ≤ 2

Answer 1

To approximate the volume with 8 boxes, we have to split up the interval of integration for each variable into 2 subintervals, [0, 1] and [1, 2]. Each box will have midpoint
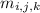`m_(i,j,k)` that is one of all the possible 3-tuples with coordinates either 1/2 or 3/2. That is, we're sampling
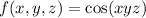`f(x,y,z)=\cos(xyz)` at the 8 points,

(1/2, 1/2, 1/2)

(1/2, 1/2, 3/2)

(1/2, 3/2, 1/2)

(3/2, 1/2, 1/2)

(1/2, 3/2, 3/2)

(3/2, 1/2, 3/2)

(3/2, 3/2, 1/2)

(3/2, 3/2, 3/2)

which are captured by the sequence

`m_(i,j,k)=\left(\frac{2i-1}2,\frac{2j-1}2,\frac{2k-1}2\right)`

with each of
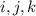`i,j,k` being either 1 or 2.

Then the integral of
`f(x,y,z)` over
`B` is approximated by the Riemann sum,

`\displaystyle\iiint_B\cos(xyz)\,\mathrm dV\approx\sum_(i=1)^2\sum_(j=1)^2\sum_(k=1)^2\cos m_(i,j,k)\left(\frac{2-0}2\right)^2`

`=\displaystyle\sum_(i=1)^2\sum_(j=1)^2\sum_(k=1)^2\cos\frac{(2i-1)(2j-1)(2k-1)}8`

`=\cos\frac18+3\cos\frac38+3\cos\frac98+\cos\frac{27}8\approx\boxed{4.104}`

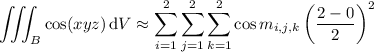
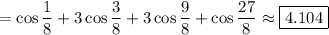
(compare to the actual value of about 4.159)