Answer:
The correct option is B.
Explanation:
The number of lattes sold daily by two coffee shops is shown in the table.
The data set for shop A is
55, 52, 56, 48, 57, 30, 45, 41
Arrange the data in ascending order.
30, 41, 45, 48, 52, 55, 56, 57
Mean of shop A is

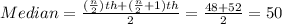
The data set for shop B is
45, 42, 57, 48, 11, 10, 46, 43
Arrange the data in ascending order.
10, 11, 42, 43, 45, 46, 48, 57
Mean of shop A is
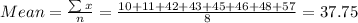
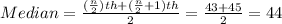
Both data distribution are not symmetric, so it is better to describe the centers of distribution in terms of median for both coffee shops. Therefore the correct option is B.