Question

The half-life of the radioactive element beryllium-13 is 5 × 10-10 seconds, and half-life of the radioactive element beryllium-15 is 2 × 10-7 seconds. The half-life of is times greater than the half-life of .

Answer 1

Answer: The half-life of beryllium-15 is 400 times greater than the half-life of beryllium-13.

Step-by-step explanation:

The half-life
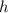`h` of a radioactive isotope refers to its decay period, which is the average lifetime of an atom before it disintegrates.

In this case, we are given the half life of two elements:

beryllium-13:
`h_(B-13)=5(10)^(-10)s=0.0000000005s`

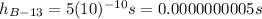
beryllium-15:
`h_(B-15)=2(10)^(-7)s=0.0000002s`

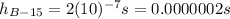
As we can see, the half-life of beryllium-15 is greater than the half-life of beryllium-13, but how great?

We can find it out by the following expression:

`h_(B-15)=X.h_(B-13)`

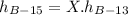
Where
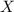`X` is the amount we want to find:

`X=(h_(B-15))/(h_(B-13))`

`X=(2(10)^(-7)s)/(5(10)^(-10)s)`

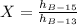
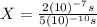
Finally:

`X=400`

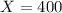
Therefore:

The half-life of beryllium-15 is 400 times greater than the half-life of beryllium-13.