Question

The combustion of titanium with oxygen produces titanium dioxide:

Ti (s) + O2 (g) → TiO2 (s)

When 2.060 g of titanium is combusted in a bomb calorimeter, the temperature of the calorimeter increases from 25.00 °C to 91.60 °C. In a separate experiment, the heat capacity of the calorimeter is measured to be 9.84 kJ/K. The heat of reaction for the combustion of a mole of Ti in this calorimeter is __________ kJ/mol.

Ti = 47.867 amu

O2 = 31.9988 amu

TiO2 = 79.8650 amu

Report answer in scientific notation use En rather than x 10n

Answer 1

The heat of reaction for the combustion of a mole of Ti in this calorimeter is
`7.769* 10^4 kJ/mol`.

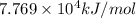Step-by-step explanation:

`Ti (s) + O_2 (g) \rightarrow TiO_2 (s)`

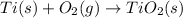
Moles of titanium =
`(2.060 g)/(47.867 g/mol)=0.04303 mol`

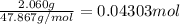
Heat absorbed by the bomb caloriometer on combustion of 0.04303 mol of titanium be Q

The heat capacity of the bomb caloriometer =c = 9.84 kJ/K

Change in temperature of the bomb caloriometer :

=ΔT=91.60 °C-25.00 °C=66.6 °C = 339.75 K

Q = c × ΔT

`Q= 9.84 kJ/K* 339.75 K=3,343.14 kJ`

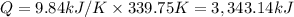
3,343.14 kJ of heat energy was released when 0.04303 moles of titanium undergone combustion.

So for 1 mol of titanium:

`(3,343.14 kJ)/(0.04303 moles)=77,693.237 kJ/mol=7.769* 10^4 kJ/mol`

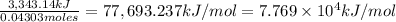
The heat of reaction for the combustion of a mole of Ti in this calorimeter is
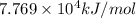`7.769* 10^4 kJ/mol`.