Question

Suppose that the number of calls coming per minute into an airline reservation center follows a Poisson distribution. Assume that the mean is 3 calls per minute. The probability that at least two calls are received in a given two-minute period is _______.

Answer 1

Answer: 0.9826

Explanation:

Given : Mean :
`\lambda =3\text{ calls per minute}`

For two minutes period the new mean would be :

`\lambda_1=2*3=6\text{ calls per two minutes}`

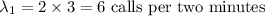
The formula to calculate the Poisson distribution is given by :_

`P(X=x)=(e^(-\lambda_1)\lambda_1^x)/(x!)`

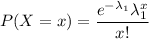
Then ,the required probability is given by :-

`P(X\geq2)=1-(P(X\leq1))\\\\=1-(P(0)+P(1))\\\\=1-((e^(-6)6^0)/(0!)+(e^(-6)6^1)/(1!))\\\\=1-0.0173512652367\\\\=0.982648734763\approx0.9826`

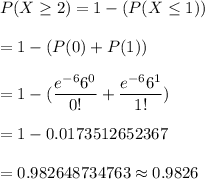
Hence, the probability that at least two calls are received in a given two-minute period is 0.9826.