1. Carl's constant rate of speed is the slope of the straight line graph.
This straight line passes through: (0,0), (5,1), (10,2) etc
We can use the slope formula with any two points to find the slope of this line.
The slope formula is
 .
.
Let
 and
and
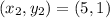
Then
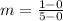 ,
,
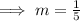 .
.
Carl's speed is
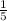 miles per minute.
miles per minute.
But we must leave our answer in miles per hour
Hence Carl's speed is
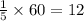 miles per hour
miles per hour
After 2 hours, Carl will travel
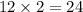 miles.
miles.
2. The given line has equation
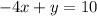
We write this in slope-intercept form by solving for y.

This is in the form
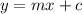 , where
, where
 is the slope.
is the slope.
When x=3,
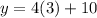
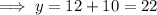
When x=3, y=22
3. The given straight line graph that models the situation passes through:
(0,0) and (20,30).
The slope of this line is
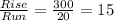
Therefore the rate is $ 15 per ticket.
If the theater sells 150 tickets, the earnings will be:
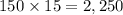 dollars.
dollars.