Answer:
20 rad/sec
Explanation:
The formula we are going to use is
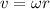
Where
v is the linear velocity (here given 60 ft/s)
 is the angular velocity (what we sought to find)
is the angular velocity (what we sought to find)
r is the radius (which is half of diameter, hence, 6/3 = 3 ft)
Plugging these numbers in, we find the angular velocity as:

Note: the units is radians per second (rad/s)
Correct answer 20 rad/sec