Answer: 478
Explanation:
The formula to calculate the standard error of the population mean is given by :-
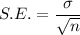 , where
, where
 is the standard deviation and 'n' is the sample size.
is the standard deviation and 'n' is the sample size.
Given: Mean :
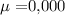
Standard deviation :
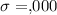
Sample size :
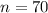
Now, the value of the standard error of the average annual salary is given by :-
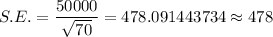
Hence, the standard error of the average annual salary = 478