Question

Which is a correct first step in solving the inequality -4(2x-1)>5-3x

Answer 1

The correct first step of solving the inequality problem -4(2x-1)>5-3x is that

Expand -4(2x-1): -8x+4

You apply the distributive laws
a=4, b=2x, c=1
= -4x time 2x-(-4) time 1

Simplify -4 time 2x+4 time 1
Multiply the numbers: 4 time2=8
= -8x+4

Multiply the numbers: 4time1=4
= -8x+4

Answer 2

Apply distributive property that's the first step.

Explanation:

The given inequality is

`-4(2x-1)>5-3x`

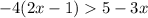
The first step we need to do is to apply distributive property to relase the binomial inside the parenthesis

`-8x+4>5-3x`

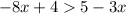
Then, we move all variables to the left side, and all constants to the right side

`-8x+3x>5-4\\-5x>1`

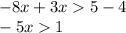
Now, we divide the inequality by -5, which changes the sign orientation

`(-5x)/(-5) <(1)/(-5)\\ x<-(1)/(5)`

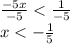
Therefore, the solution is a set with all values less than -1/5. The graph attached shows this solution.