Question

The area of a bulletin board is 52 square feet the length is three feet less than four times the width find the length and width of the bulletin board

Answer 1

The length of the bulletin board is 13\ ft
The width of the bulletin board is 4\ ft

Answer 2

Length: 13 feet,

Width: 4 feet.

Explanation:

Let w represent width of bulletin board.

We have been given that the length is 3 feet less than 4 times the width. So the length of the bulletin board would be
`4w-3`.

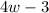We have been given the area of a bulletin board is 52 square feet. We know that a bulletin board is in form of rectangle, so its area would be length times width.

We can represent this information in an equation as:

`w(4w-3)=52`

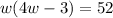
Let us solve for w.

`w(4w-3)=52`

`4w^2-3w=52`

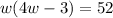
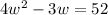
Use quadratic formula:

`w=(-(-3)\pm√((-3)^3-4\cdot 4\cdot (-52)))/(2\cdot 4)`

`w=(3\pm√(9+832))/(8)`

`w=(3\pm√(841))/(8)`

`w=(3\pm29)/(8)`

`w=(3-29)/(8)\text{ (or) }w=(3+29)/(8)`

`w=(-26)/(8)\text{ (or) }w=(32)/(8)`

`w=(-13)/(4)\text{ (or) }w=4`

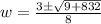
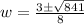
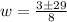
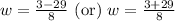
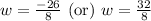
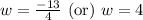
Since width cannot be negative, therefore, width of the bulletin board is 4 feet.

Substitute
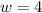`w=4` in expression
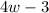`4w-3` to find length of bulletin board.

`4w-3\Rightarrow 4(4)-3=16-3=13`

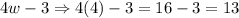
Therefore, length of the bulletin board is 13 feet.