Question

Hans wanted to find the length of the hypotenuse of the triangle. Which statement correctly identifies his error?

Answer 1

He did not square 40, he just multiplied by 2.

EXPLANATION

According to the Pythagoras Theorem, the sum of the square of the shorter legs equals the square of the Hypotenuse.

Hans correctly applied the Pythagoras Theorem to obtain:

`{9}^(2) + {40}^(2) = {c}^(2)`

The next correct step is to evaluate the squares to obtain:

`9 * 9+ {40} * 40= {c}^(2)`

Which gives

`81+1600= {c}^(2)`

But Hans mistakenly multiplied the exponent of the second square by the base to get

`9 * 9+ {40} *2= {c}^(2)`

Which simplifies to;

`81+ 80= {c}^(2)`

Therefore the error is that,he did not square 40, he just multiplied by 2.

The first choice is correct.

Answer 2

Error: He did not square 40, he multiplied by 2

In calculation of 40² ( Correct was 1600 but he did 80)

The length of hypotenuse is 41 cm

Explanation:

Given: In the given right angle triangle.

The two legs are 40 and 9.

The hypotenuse is c

Using Pythagoras theorem,

`c^2=a^2+b^2`

where, a and b are legs and c is hypotenuse

a=40 , b=9

Substitute into formula

`c^2=40^2+9^2`

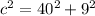
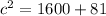`c^2=1600+81` Error

Hans did mistake here to calculate square of 40.

instead of square Hans multiply 40 and 2.

`c^2=1600+81`

`c^2=1681`

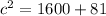
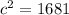
Taking square root

`c=√(1681)`

`c=41`

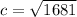
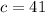
Hence, The length of hypotenuse is 41 cm

Error: In calculation of 40²