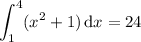Splitting up the interval [1, 4] into 6 equally-spaced subintervals gives the partition
[1, 3/2], [3/2, 2], [2, 5/2], [5/2, 3], [3, 7/2], and [7/2, 4]
each with length (4-1)/6 = 1/2.
The endpoints of each subinteval form arithmetic sequences,
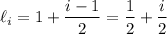
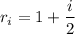
(
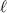 for left,
for left,
 for right) with
for right) with
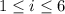 .
.
The midpoints of each subinterval are, respectively,
5/4, 7/4, 9/4, 11/4, 13/4, and 15/4
which are prescribed by the sequence,
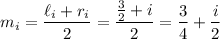
(
 for midpoint) where
for midpoint) where
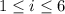 .
.
The integral of
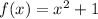 over the interval [1, 4] is approximated by the sum of the areas of rectangles with length equal to the base of each subinterval and height equal to
over the interval [1, 4] is approximated by the sum of the areas of rectangles with length equal to the base of each subinterval and height equal to
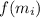 , the value of
, the value of
 at the midpoint of that subinterval:
at the midpoint of that subinterval:
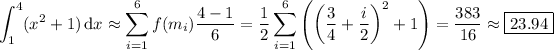
Compare to the actual value of the integral,