Answer: 2401
Explanation:
Formula to find the sample size is given by :-
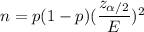
, where p = prior population proportion.
 = Two -tailed z-value for
= Two -tailed z-value for
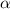
E= Margin of error.
As per given , we have
Confidence level :
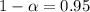
⇒

Two -tailed z-value for
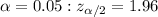
E= 2%=0.02
We assume that nothing is known about the percentage of computers with new operating systems.
Let us take p=0.5 [we take p= 0.5 if prior estimate of proportion is unknown.]
Required sample size will be :-
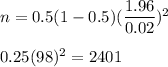
Hence, the number of computer must be surveyed = 2401