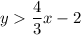Answer:
Option: C is the correct answer.
C.
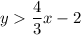
Explanation:
By looking at the graph we observe that the line is dotted this means that the inequality will be strict.
Also, this line passes through the point (-3,-6) and (3,2).
Hence, the equation of line is calculated by using a two point form i.e. a line passing through two points (a,b) and(c,d) is calculated with the help of formula as:
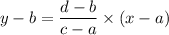
Here (a,b)=(-3,-6) and (c,d)=(3,2)
i.e.
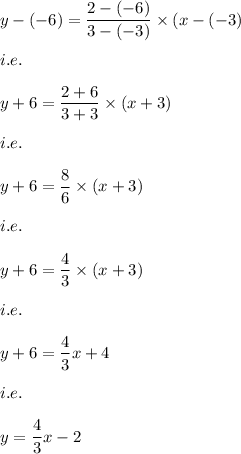
Also, the shaded region is towards the origin.
Hence, the inequality is: