Question

What are the possible numbers of positive, negative, and complex zeros of f(x) = −3x4 −

5x3 − x2 − 8x + 4?

Select one:
a. Positive: 2 or 0; negative: 2 or 0; complex: 4 or 2 or 0
b. Positive: 1; negative: 3 or 1; complex: 2 or 0
c. Positive: 3 or 1; negative: 1; complex: 2 or 0
d. Positive: 4 or 2 or 0; negative: 2 or 0; complex: 4 or 2 or 0

Answer 1

b.

Explanation:

We have to look at sign changes in f(x) to determine the possible positive real roots.

`f(x)=-3x^4-5x^3-x^2-8x+4`

There is only one sign change here, between the -8x and the +4. So that means there is only 1 possible real positive root.

Now we have to look at sign changes in f(-x) to determine the possible negative real roots.

`f(-x)=-3x^4+5x^3-x^2+8x+4`

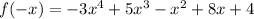
There are 3 sign changes here. That means there are either 3 negative roots or 3-2 = 1 negative root. So we have:

1 positive

3 or 1 negative

We need to pair them up now with all the possible combinations.

If we have 1 positive and 1 negative, we have to have 2 imaginary

If we have 1 positive and 3 negative, we have to have 0 imaginary

Keep in mind that the total number or roots--positive, negative, imaginary--have to add up to equal the degree of the polynomial. This is a 4th degree polynomial, so we will have 4 roots.