Question

The roots of the equation 2×^2 + 3x -4=0 are a and b.
find the values of

a^2ß^2​

Answer 1

4

Explanation:

given a quadratic equation in standard form

y = ax² + bx + c = 0 : a ≠ 0

with roots α and β, then

the sum of the roots α + β = -
`(b)/(a)` and

the product of the roots αβ =
`(c)/(a)`

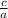
2x² + 3x - 4 = 0 ← is in standard form

with a = 2, b = 3 and c = - 4

αβ =
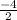`(-4)/(2)` = - 2, hence

α²β² = (αβ)² = (- 2)² = 4

Answer 2

hello : a²b² =4

Explanation:

2ײ + 3x - 4=0

The roots of this equation exist because (2)(-4)<0

note : a'x²+b'x +c' =0.......The roots of this equation : a and b

a×b = c'/a' a' =2 and b'=3 and c' = - 4

in this exercice ; a²b² = (ab)² = (c'/a')² = (-4/2)² = (-2)² =4