Question

The passing yards for the top 5 quarterbacks in the country are 3,832, 3,779, 3,655, 3,642, and 3,579. Find the variance and standard deviation. Round to the nearest hundredth.

(EXPLAIN WORK)

Answer 1

Variance = 8732.24 and standard deviation = 93.45

Step-by-step explanation:

We have to calculate the variance and standard deviation of the data set

3,832, 3,779, 3,655, 3,642, 3,579

First we calculate the mean of the data

Mean =
`((3,832+3,779+3,655+3,642+3,579))/(5)`

=
`(18487)/(5)`

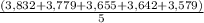
= 3697.4

Now we calculate the variance by subtracting the mean from value of data set and square it.

3832 - 3697.4 = 134.6² = 18,117.16

3779 - 3697.4 = 81.6² = 6,658.56

3655 - 3697.4 = -42.4² = 1,797.76

3642 - 3697.4 = -55.4 = 3069.16

3579 - 3697.4 = -118.4 = 14,018.56

Add up the squared result and take the mean

=
`((18117.16+6658.56+1797.76+3069.16+14018.56))/(5)`

=
`(43661.2)/(5)`

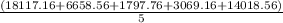
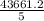
Variance = 8732.24

To calculate standard deviation, we take the square root of the variance =
`√(8732.24)`

Standard deviation = 93.44645526 ≈ 93.45

Variance = 8732.24 and standard deviation = 93.45

Answer 2

Answer:

• variance = 8,732.24

• standar deviation = 93.45

Step-by-step explanation:

In order to calculate the variance and standard deviation of a set of data, you first must calculate the mean.

Mean = average = μ = ∑ values / (number of data)

Hence, the mean of our data set is:

• mean = μ = [ 3,832 + 3,779 + 3,655 + 3,642 + 3,579] / 5 = 18,487 / 5 = 3,697.4

Now you can calcuate the variance using the formula.

For a data set (which is all your population and not a sample) the formula is:

• Variance = ∑ (value - μ)² / (number of data)

That is:

• Variance = [ (3,832 - 3,697.4)² + (3,779 - 3,697.4)² + (3,655 - 3,697.4)² + (3,642 - 3,697.4)² + (3,579 - 3,697.4)² ] / 5

• Variance = 8,732.24 (rounded to the nearest hundreth)

The standard deviation, S.D., is the square root of the variance:

• 
  `S.D.=√(8,732.24)=93.45` (rounded to the nearest hundresth)