Question

How will the solution of the system change if the inequality sign on both inequalities

Answer 1

Shown below

Explanation:

The first system of inequality is the following:

`\left\{ \begin{array}{c}y>2x+(2)/(3)\\y<2x+(1)/(3)\end{array}\right.`

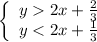
To find the solution here, let's take one point, say,
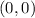`(0,0)` and let's taste this point into both inequalities, so:

FIRST CASE:

First inequality:

`y>2x+(2)/(3) \\ \\ 0>2(0)+(2)/(3) \\ \\ 0>(2)/(3) \ False!`

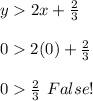
The region is not the one where the point
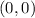`(0,0)` lies

Second inequality:

`y<2x+(1)/(3) \\ \\ 0<2(0)+(1)/(3) \\ \\ 0<(1)/(3) \ True!`

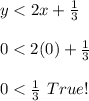
The region is the one where the point
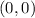`(0,0)` lies

So the solution in this first case has been plotted in the first figure. As you can see, there is no any solution there

SECOND CASE:

First inequality:

`y<2x+(2)/(3) \\ \\ 0<2(0)+(2)/(3) \\ \\ 0<(2)/(3) \ True!`

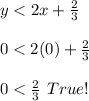
The region is the one where the point
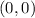`(0,0)` lies

Second inequality:

`y>2x+(1)/(3) \\ \\ 0>2(0)+(1)/(3) \\ \\ 0>(1)/(3) \ True!`

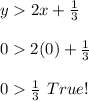
The region is not the one where the point
`(0,0)` lies

So the solution in this first case has been plotted in the second figure. As you can see, there is a solution there.

CONCLUSION: Notice that when reversing the signs on both inequalities the solution in the second case is the part of the plane where the first case didn't find shaded region.