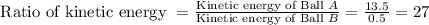Question

If the mass of a ball B is 1 kilogram and it’s speed is 1 m/sec. the mass and the speed of ball A is three times the mass and speed of ball B. What is the ratio of kinetic energy of ball A to ball B? Hint: dividethe kinetic energy equation for ball A by the kinetic energy equation of ball B.

A.3
B.6
C.9
D.27

Answer 1

your answer would be 27.

Answer 2

The ratio of kinetic energy of ball A to ball B is 27

Answer: Option D

Explanation:

The kinetic energy of any object is the energy exhibited by the object when it is in motion. The kinetic energy of any object is directly proportional to the mass of the object and square of the speed at which the object is moving. So the kinetic energy of any object can be represented as

`E_(k)=(1)/(2) * m *(\text { speed })^(2)`

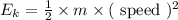
In this case, for ball B the mass is 1 kg and speed is 1 m/s. So the kinetic energy of ball B is

`\text { Kinetic energy for ball } B=(1)/(2) * 1 * 1^(2)=0.5 J`

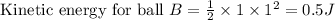
As it is said that the mass (M) and speed of ball A is three times the mass and speed of ball B. So ,

`\text { M of ball } A=3 * M \text { of ball } B=3 * 1=3 \mathrm{kg}`

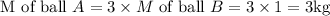
And,

`\text { Speed of ball } A=3 * \text { Speed of ball } B=3 * 1=3 \mathrm{m} / \mathrm{s}`

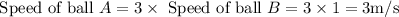
Thus, the kinetic energy of ball A will be

`\text {Kinetic energy for ball } A=(1)/(2) * 3 * 9=13.5 \mathrm{J}`

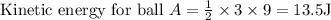
Now, to determine the ratio of kinetic energy of ball A to ball B,

`\text { Ratio of kinetic energy }=\frac{\text {Kinetic energy of Ball } A}{\text {Kinetic energy of Ball } B}=(13.5)/(0.5) = 27`