Question

Andy is learning to play the guitar. Last week he recorded the minutes per day that he practiced. Find the mean absolute deviation. Round to the nearest tenth.

Day S M T W T F S
Minutes 40 55 35 60 20 50 55

Answer 1

11.4

Explanation:

Step 1: Calculate the mean.

40, 55, 35, 60, 20, 50, 55

=

315

divided by 7

=

45

Step 2: Calculate how far away each data point is from the mean using positive distances. These are called absolute deviations.

40 - 45 = 5

55 - 45 = 10

35 - 45 = 10

60 - 45 = 15

20 - 45 = 25

50 - 45 = 5

55 - 45 = 10

Step 3: Add those deviations together.

= 80

Step 4: Divide the sum by the number of data points.divided by 7

= 11.428

Step 5: Round to the nearest tenth.

= 11.4

Answer 2

The mean absolute deviation is approximately is 11.43.

Explanation:

The means absolute deviations is define by:

`D_(x) =(\sum |x_(i)-x| )/(N)`

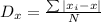
From the formula, we observe that we need to find the mean, and then find the different between that mean and each element. Then, we have to sum all those differences and divide this by the total number of elements.

So, the mean is

`x=(\sum x_(i) )/(N)\\ x=(40+55+35+60+20+50+55)/(7)=45`

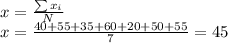
Now, each difference would be

`40-45=-5\\55-45=10\\35-45=-10\\60-45=15\\20-45=-25\\50-45=5\\55-45=10`

The sum of all differences, using their absolute value, would be:

`5+10+10+15+25+5+10=80`

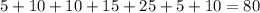
Then, we divide this result by the total number of elements which is 7:

`(80)/(7) \approx 11.43`

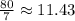
Therefore, the mean absolute deviation is approximately is 11.43.