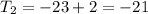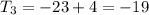Answer:
1).
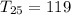
2).

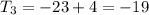
Explanation:
First term of an arithmetic sequence is (-1) and common difference is 5.
Then we have to find twenty fifth term of this arithmetic sequence.
Since explicit formula of an arithmetic sequence is represented by
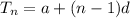
Where
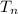 represents nth term of the sequence.
represents nth term of the sequence.
a = first term
n = number of term
and d = common difference
Now we will find 25th term of this sequence.
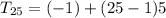
= (-1) + 120
= 119
Similarly in second part of this question we have to find first three terms of an arithmetic sequence in which
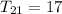 and
and
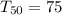
Now from the explicit formula
17 = a + (21 - 1)d
17 = a + 20d --------(1)
75 = a + (50 - 1)d
75 = a + 49d --------(2)
Now we subtract equation 1 from 2
75 - 17 = 49d - 20d
29d = 58
d =
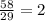
By putting d = 2 in equation 1
17 = a + 20×2
17 = a + 40
a = 17 - 40
a = -23
Therefore, first three terms of this sequence will be