Question

A beach ball with a volume of 5,000 cm3 is pushed underwater. What is the magnitude of the buoyant force pushing upwards? The density of water is 1 gram/cm3. 49N 25N 40N 39N

Answer 1

Hello!

The answer is:

The buoyant force is equal to 49N.

Why?

The buoyant force is the force that pushes upwards and object when it's submerged in water, this force is always trying to move the object to the surface of the liquid or water. We must consider that the volume of water or liquid displaced is equal to the volume of the submerged object.

We can calculate the buoyant force using the following formula:

`F_(B)=Density*VolumeDisplaced*GravityAcceleration`

Where,

Density is the density of the water or liquid.

Volume displaced is equal to the volume of the submerged object.

Gravity acceleration is the acceleration due to gravity.

So, from the statement we know that:

`VolumeDisplaced=BeachBallVolume=5000cm^(3)\\\\Density=1(gram)/(cm^(3) )=(0.001kg)/(cm^(3) )\\\\g=9.8(m)/(s^(2) )`

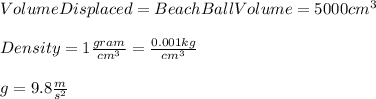
Now, substituting and calculating we have:

`F_(B)=Density*VolumeDisplaced*GravityAcceleration`

`F_(B)=0.001(kg)/(cm^(3)*) *5000cm^(3)*9.8(m)/(s^(2) )`

`F_(B)=0.001(kg)/(cm^(3)*) *5000cm^(3)*9.8(m)/(s^(2) )`

`F_(B)=49(Kg.m)/(s^(2))=49N`

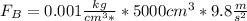
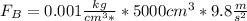
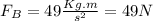
Hence, we have that the correct answer is:

The buoyant force is equal to 49N.

Have a nice day!