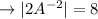Answer with explanation:
For, a 3 × 3, matrix
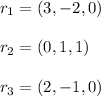
which are entries of First, Second and Third Row Respectively.
So, if written in the form of Matrix (A)
![A=\left[\begin{array}{ccc}3&-2&0\\0&1&1\\2&-1&0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/j4drbg1277jsgfuvwdapmso46wu5yzp51l.png)
⇒Adjoint A= Transpose of Cofactor of A
![a_(11)=1,a_(12)=2,a_(13)=-2\\\\a_(21)=0,a_(22)=0,a_(23)=-1\\\\a_(31)=-2,a_(32)=- 3,a_(33)=3\\\\Adj.A=\left[\begin{array}{ccc}1&0&-2\\2&0&-3\\-2&-1&3\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/guf7kxq1jb84qy8wuysoe7i6p4jm5rkogy.png)
⇒≡ |Adj.A|=1 ×(0-3) -2×(-2-0)
= -3 +4
=1 --------(1)
⇒For, a Matrix of Order, 3 × 3,
| Adj.A |=| A|²---------(2)
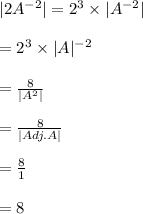
--------------------------------------------(Using 1 and 2)