Question

2. An investment company pays 9% compounded semiannually. You want to have $8,000 in the future. How much should you deposit now to have that money 5 years from now?

Answer 1

$5151.42

Explanation:

The formula you need is

`A(t)=P(1+(r)/(n))^((n)(t))`

where A(t) is the amount after the compounding, P is the initial investment, r is the interest rate in decimal form, n is the number of compoundings per year, and t is time in years. The info we have is

A(t) = 8000

P = ?

r = .09

t = 5

Filling in we have

`8000=P(1+(.09)/(2))^((2)(5))`

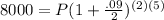
Simplifying a bit and we have
`8000=P(1+.045)^(10)`

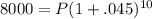
Now we will add inside the parenthesis and raise 1.045 to the 10th power to get

8000 = P(1.552969422)

Divide away the 155... on both sides to solve for P.

P = $5151.42