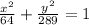Question

An ellipse has vertices at (0, #17) and foci at (0, ±15). Write the equation of the ellipse in standard form. Graph the ellipse.

Answer 1

`\frac{ {x}^(2) }{ 64 } + \frac{ {y}^(2) }{ 289 } = 1`

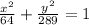
See attachment for the graph

Step-by-step explanation

The standard equation of the vertical ellipse with center at the origin is given by

`\frac{ {x}^(2) }{ {b}^(2) } + \frac{ {y}^(2) }{ {a}^(2) } = 1`

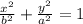
where

`{a}^(2) \: > \: {b}^(2)`

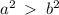
The ellipse has its vertices at (0,±17).

This implies that:a=±17 or a²=289

The foci are located at (0,±15).

This implies that:c=±15 or c²=225

We use the following relation to find the value of b²

`{a}^(2) - {b}^(2) = {c}^(2)`

`\implies \: 289 - {b}^(2) = 225`

`- {b}^(2) = 225 - 289`

`- {b}^(2) = - 64`

`{b}^(2) = 64`

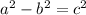
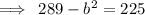
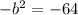
We substitute into the formula for the standard equation to get:

`\frac{ {x}^(2) }{ 64 } + \frac{ {y}^(2) }{ 289 } = 1`