Question

What is the present value of ​$3,000 per year for 9 years discounted back to the present at 10 ​percent?

Answer 1

$17,277.07

Explanation:

Present value of annuity is the present worth of cash flow that is to be received in the future, if future value is known, rate of interest is r and time is n then PV of annuity is

PV of annuity =
`(P[1-(1+r)^(-n)])/(r)`

=
`(3000[1-(1+0.10)^(-9)])/(0.10)`

=
`(3000[1-(1.10)^(-9)])/(0.10)`

=
`(3000[1-0.4240976184])/(0.10)`

=
`(3000(0.5759023816))/(0.10)`

=
`(1,727.7071448)/(0.10)`

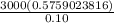
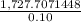
= 17,277.071448 ≈ $17,277.07